Algebraic expressions that we see and encounter today is way different than it was centuries ago. Until 19th century, they consisted of theories. The father of algebra Muhammad ibn Musa al-Khwarizmi described algebra to be reduction and balancing of terms that is a transposition to other sides of the equation. Algebra went through different stages to development along the centuries. Along which the three stages that gives us the history of symbolic algebra are to be discussed in this article.
1. RHEOTORICAL STAGE
In this stage, the algebraic expressions were written in
sentences. For example, an equation as: x+ 24= 36 would be described as
‘something added to 24 gives us 36’. It was developed by Babylonians back in
the 16th century.
2. SYNCOPATED ALGEBRA
In this stage, the symbolism was used but it didn’t
contain all of the characteristics of symbolic algebra, there were some
restrictions involved. Syncopated algebra made its first appearance in the 3rd
century AD through Diophantus Arithmetic, followed by Brahmgupta’s Brahma
Sphuta Siddhanta back in the 7th century.
3. SYMBOLIC ALGEBRA
Symbolic algebra made its appearance through Islamic mathematicians such as Ibn al-Banna in 13-14th centuries and al-Qalasadi in 15th century in their works. And it was fully developed by Francois Viete in the 10th century. Later, Rene Descartes by 17th century, introduced the use of ‘x’ in an equation. He also showed that problem in geometry can be expressed and solved in terms of algebra. Quadratic equations played an important role in early algebra and it is to be noted that earlier only three types of quadratic equations existed:
Since math was used in commerce there were no use of
negative terms. ‘p’ and ‘q’ was positive in each of the above cases and so were
the roots.
On to most interesting part where mathematical
expressions were solved with geometric practices. Between the rheotorical and
syncopated stage of symbolic algebra, the geometric constructive algebra’ was
developed by classical Greek and Vedic Indian Mathematicians in which equations
were solved through geometry.
Now let’s look at this equation:
Since we already know how to find roots of quadratic
equation, i.e. by using,
As they didn’t consider the negative part, let us
exclude that and put the respective values, we will get
And now let’s solve it with the help of figures. Taking
the x^2 as a square of side x and thus the term gives its area.
And the 26x can be denoted as rectangle with sides 26 and x and the term being
the area.
Now, if we divide the rectangle into two equal parts
which will give us two rectangle of side x and 13.
By placing the rectangles on two adjacent sides of the
square, we will see a L shaped figure which can we converted into a square if
we added a square of side 13 in the space.
And since we added a square, we now have to add 169, which
is the area of the additional square, on each sides of the equation. It gives
us
The left-hand side of the equation represents the sum of areas of the 2 squares and 2 rectangle and the right-hand side gives the total area. Since all the shapes collectively makes a square, the number 246 denotes the area of the biggest square. And hence 14 will be the length of the sides. And now we know that the value of x must be 1.
While this method will only work on positive
entities and will only give the positive part of the solution, we can now see the quadratic equations from a whole new perspective.






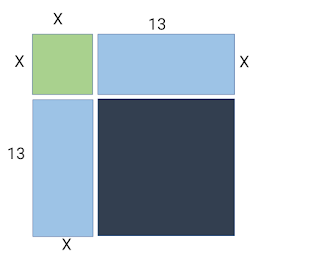





0 Comments